Violão

Campo Harmônico

            
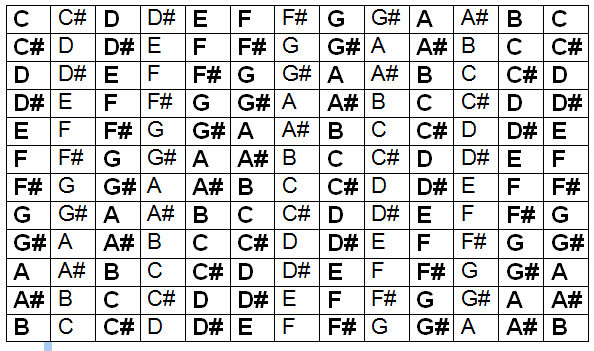
Chamamos de campo harmônico o conjunto de acordes que acompanha determinada tonalidade. Tais acordes são extraídos de cada intervalo da escala maior.

              
Escala                                               Campo harmônico

C – D – E – F – G – A – B                 C – Dm – Em – F – G – Am – Bm5-

C# – D# – F – F# – G# – A# – C        C# – D#m – Fm – F# – G# – A#m – Cm5-

D – E – F# – G – A – B – C#             D – Em – F#m – G – A – Bm – C#m5-

D# – F – G – G# – A# – C – D            D# – Fm – Gm – G# – A# – Cm – Dm5-

E – F# – G# – A – B – C# – D#          E – F#m – G#m – A – B – C#m – D#m5-

F – G – A – A# – C – D – E                 F – Gm – Am – A# – C – Dm – Em5-

F# – G# – A# – B – C# – D# – F         F# – G#m – A#m – B – C# – D#m – Fm5-

G – A – B – C – D – E – F#                  G – Am – Bm – C – D – Em – F#m5-

G# – A# – C – C# – D# – F – G           G# – A#m – Cm – C# – D# – Fm – Gm5-

A – B – C# – D – E – F# – G#                A – Bm – C#m – D – E – F#m – G#m5-

A# – C – D – D# – F – G – A                 A# – Cm – Dm – D# – F – Gm – Am5-

B – C# – D# – E – F# – G# – A#      B – C#m – D#m – E – F# – G#m – A# m5-

Tom Relativo menor:

Para cada acorde maior natural temos um acorde menor que estabelece relação direta com este. Tal acorde possui características semelhantes ao tom maior (repete tônica e terça), por este motivo chamamos de Relativo Menor. No campo harmônico, o relativo menor será sempre encontrado no 6º grau.

Vejamos o exemplo:                                                                                            

1º C = C – E - G      

2º Dm = D – F - A     

3º Em = E – G - B     

4º F = F – A - C  

5º G = G – B - D   

6º Am = A – C – E            

7º Bm(5-) = B – D - F

Note que no acorde de dó (C) as notas fundamentais são a Tônica (C) e a Terça (E) que define se o acorde é maior ou menor. Bem, acontece que no campo harmônico de dó, tais notas encontram-se no acorde de dó (C) e lá menor (Am). Portanto, dizemos que Am é relativo de C.

Relativos menores em todas as tonalidades

C / Am          C# / A#m           Db / Bbm           D / Bm

D# / Cm        Eb / Cm             E / C#m              F / Dm

F# / D#m      Gb / Ebm           G / Em                G# / Fm

Ab / Fm        A / F#m              A# / Gm              Bb / Gm

B / G#m

 Escalas
Uma sequência ordenada de notas pela frequência vibratória de sons, (normalmente do som de frequência mais baixa para o de frequência mais alta), que consiste na manutenção de determinados intervalos entre as suas notas.

As escalas musicais formam a base necessária para a formação de acordes e tonalidades. 
Escala Cromática

Formada por 12 sons diferentes, a escala cromática é separada somente por intervalos de ½ tom, contendo as 7 notas musicais e 5 acidentes formados por sustenidos (#), no sentido ascendente,  ou bemóis (b), no sentido descendente. Assim temos:

C - C# - D - D# - E - F - F# - G - G# - A - A#  - B

Escala Maior Natural

A escala maior natural, diferentemente da cromática, é formada por intervalos de tom e semitom. Essa escala possui 7 notas e 8 graus, já que a tônica se repete ao final. Por isso, a chamaremos de diatônica. 

Este padrão será seguido para formarmos todas as escalas maiores, conforme tabela a seguir.

Adicionar legenda

TRÍADES

Para formarmos um acorde natural, maior ou menor, precisamos de 3 notas da escala maior. A isso damos o nome de tríade.

TRÍADE MAIOR

É formada com a utilização do 1º o 3º e o 5º graus da escala. Veja o exemplo:

Assim temos:

C= C – E – G                   C#= C# - F – G#

D= D – F# - A                  D#= D# - G – A#

E= E – G# - B                  F= F – A – C

F#= F# - A# - C#             G= G – B – D

G#= G# - C – D#             A= A – C# - E

A#= A# = D – F                B= B – D# - F#

TRÍADE MENOR

A exemplo da tríade maior, também é formada com a utilização do 1º o 3º e o 5º graus da escala. Contudo, neste caso o 3º grau da escala é bemolizado ( diminuído em ½ tom), tornando-se menor. Veja o exemplo:

Assim temos:                                     

Cm= C – Eb – G              C#m= C# - E – G#

Dm= D – F - A                  D#m= D# - Gb – A#

Em= E – G - B                  Fm= F – Ab – C

F#m= F# - A - C#             Gm= G – Bb – D

G#m= G# - B – D#           Am= A – C - E

A#m= A# = Db – F           Bm= B – D - F#